Support Vectors Machines
An Introduction to Support Vectors; Hyperplanes, Margins and Dimensions.
This week, we step even further, into Machine Learning… by studying SVMs - Support Vector Machines. If you intend to follow along, It’s necessary you're already familiar with stuff we’ve discussed in previous weeks.
Ideally, you wanna be familiar with the concept of Machine Learning. You need to understand the different paradigms or types of machine learning, and the terminologies associated with them.
Through our knowledge on those, we shall understand where the application of support vector machines is most appreciated.
What is SVM?
Support Vector Machines (SVMs) are supervised machine learning models used mainly for classification but can sometimes also be used for regression. The main goal of SVMs is to find the best boundary (called the hyperplane) that separates data points of different classes
Imagine you're organizing a party, and you have two types or groups of guests. And you want to make sure these two groups are seated far apart to avoid a fight. To do this, you draw an imaginary line (or plane) that separates the two groups in the room. Your goal is to make sure the line is as far as possible from both groups, maximizing the peace in the room. This line is called a decision boundary.
In the world of Machine Learning, this is what SVM does:
It tries to find the best boundary (called the hyperplane) to separate two groups of data.
The hyperplane is chosen so that the gap (or margin) between the two groups is the largest possible.
Then, to properly classify both groups and along correctly predicting what group a new data point (new guest) would belong to.
Key Concepts of SVM
Hyperplane:
It's the boundary that separates data points belonging to different classes.
In 2D, it’s a line. In 3D, it’s a plane. In higher dimensions, it’s a “hyperplane.”
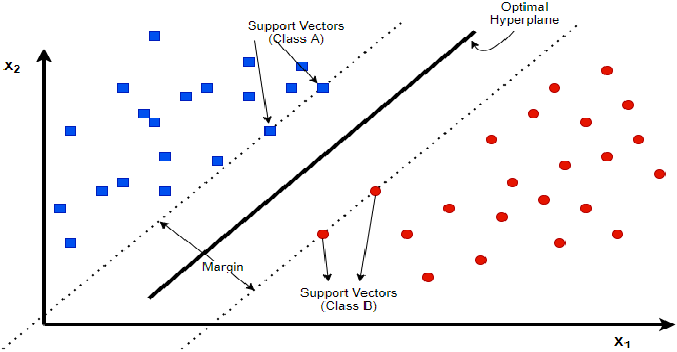
Support Vectors:
These are the data points that are closest to the hyperplane. They are the “supporting players” that help define the position and orientation of the hyperplane.
If these points moved, the hyperplane would change.
Margin:
The distance between the hyperplane and the nearest data points from each class.
SVM maximizes this margin to ensure good separation.
This Figure illustrates the positions of the key concepts of SVM highlighted above.
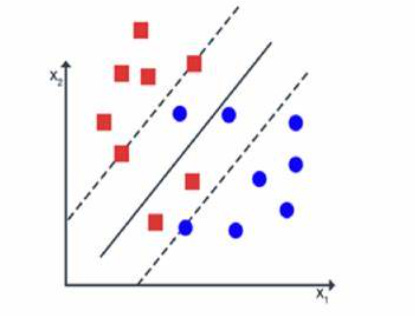
Hard Margin Classification
The figure above, illustrates a perfect case of Hard Margin Classification.
It works when data is no overlap between classes and data is linearly separable, meaning that a straight line, (or a flat hyperplane in higher dimensions) can separate the classes without error.
The goal of a Hard Margin Classification is to find a hyperplane that most accurately separates the classes with the maximum margin.
Even though the Hard Margin works well when the data is clearly separable, it does have a few limitations…
Outliers can ruin the model - Even a single noisy point can prevent finding a valid hyperplane.
Rigid - No tolerance for misclassified points.
Basically, only works well when there’s no noise or outliers in the data.
Soft Margin Classification, on the other hand, is used when:
Data isn’t perfectly separable due to noise or overlapping classes.
A small number of misclassifications is allowed to improve generalization.
(Refer to the image below)
Notice how, regardless of how spread-out and overlapping
the data points are, the soft margin still somehow decently show where the optimal hyperplane should be.
Key Features:
Balances two goals:
Maximizing the margin.
Allowing some points to be on the wrong side of the hyperplane.
Measure how much a point violates the margin through something called slack variables.
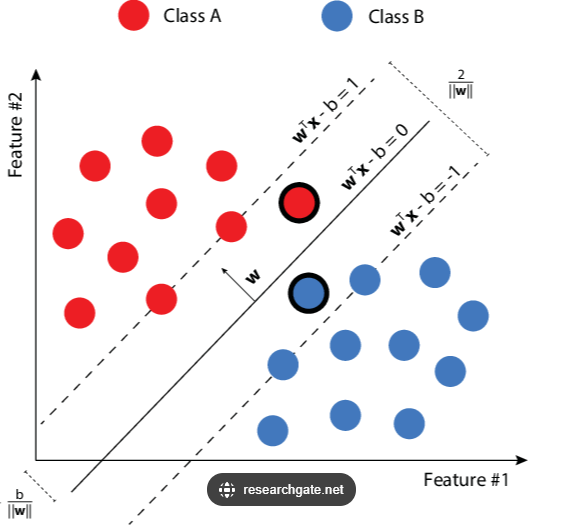
It is great to note that mathematically, the hyper plane is expressed as
Where…
w is a weight vector [w1,w2] determining the orientation or angle of the hyperplane.
x represents the input features. In a 2D dimension, we could have [x1,x2]
b is the bias term that shifts the hyperplane. It moves the hyperplane up and down.
In practice, applying Support Vector Machines (SVMs) is straightforward, thanks to the powerful and user-friendly scikit-learn library in Python.
It makes abstract, the complexities of SVM mathematics and optimization, allowing you to focus on data preparation, model training, and evaluation.
However, it is necessary to get a good grasp of the underlying logic as it aids in tuning and setting the necessary parameters for desired performance.
Following up, we shall see how SVMs can be used to handle non-linear data using Kernel Tricks.
By basically mapping it to higher-dimensional spaces and transforming the data into a space where it becomes linearly separable, kernels unlock the full potential of SVMs for solving complex, non-linear problems.
We look forward to understanding how kernels work, some common kernels, and how we can choose the right kernel for our data.
Cheers! :)